НАЈВАЖНИОТ НЕРЕШЕН ПРОБЛЕМ НА КОМПЈУТЕРЏИИТЕ Кој ќе го пробие ова добива милион долари…

Еден нерешен проблем на милениумот може да им ги отвори вратите на компјутерџиите – решавајќи го него можат да ги решат и другите шест, а секој од проблемите вреди милион долари. Барем толку за решавањето понуди Институтот за математика Клеј во 2000 година, пишува Американска наука.

Но, настрана парите, она што би можел овој проблем да им каже на програмерите е многу подлабоко. Прашањето гласи:

„Ако е лесно да провериме готови дадени решенија за најсложените проблеми, тогаш зошто не би било лесно и да ги решиме најсложените проблеми? Дали постои асимтерија меѓу овие две нешта или се исти?“

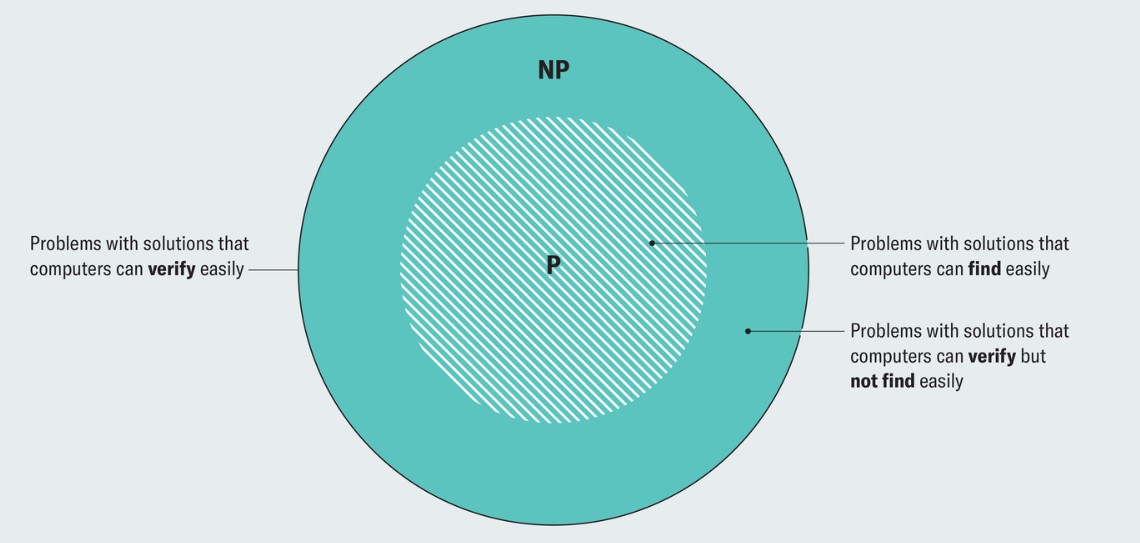
Проблемот популарно се вика П наспроти НП. П е множество од проблеми кои компјутерите ги решаваат ефикасно, како сортирање колона од броеви во табела или наоѓање на најкратката патека помеѓу две адреси на карта. НП, од друга страна, е множеството на проблеми за кои компјутерите можат само да проверуват решенија.

Со други зборови, П е кога решавате некој проблем директно, а НП е кога, не знаејќи како да го решите проблемот, нудите разни одговори, под а), под б), под ц) и потоа проверувате дали некој од одговорите одговара за решение.

Второто изгледа потешко, односно подолго, бидејќи проверувате од решение до решение и навидум е логично дека НП е поголемо множество од П. Но, дали е тоа така и како да се докаже?

Она што ги зачудува компјутерџиите и математичарите е дека сложените проблеми иако се сложени, кога веќе еднаш ќе ги решите, или ќе понудите решение за нив, брзо можат да бидат проверени во нивната точност.

Замислете дека сте напишале книга бестселер и дека планирате светска турнеја во многу градови и барате како најевтино да ги резервирате летовите со авион за да стигнете до сите места. Проблемот е сложен затоа што има многу рути и летови, многу комбинации кои можете да ги направите.

Па сепак, ако некој од страна ви каже дека го нашол решението и ви понуди готова рута која тој смета дека е најоптималната, вие потоа лесно може да проверите дали рутата е точна, односно дали го опфаќа секој град што планирате да го посетите.

Си велите, чекај, можам да напишам алгоритам кој со кратенка, со некаква равенка или збир од равенки ќе избегне да треба да проверува милиони решенија и ќе ги провери само тие кои се оптимални…Но, многу често постојат нерешливи проблеми, нерешливи и поради комплексноста и поради обемот.

Начинот на којшто П и НП најчесто се прикажани е како множества, со тоа што П е дел од НП. Тоа е затоа што за да решите еден проблем, а не само да проверувате од можни готови решенија, е исто како да сте ги провериле сите можни решенија за проблемот и сте дошле до точното.

Значи, П е подмножество на НП. Но, постојат проблеми кои се дел од НП, а не се дел од П. Овие проблеми ги мачат научниците. Тоа се проблемите за кои не знаеме ниту дали може да постои алгоритам за решавање.

И тука доаѓаме до уште еден проблем. Што е алгоритам? За да имате алгоритам кој решава судоку тој треба да може да ги решава сите можни судокуа на светот. Исто како да ги има проверено решенија. Значи треба да биде и П и НП? Значи, можеби П не е само подмножество на НП и нивниот однос е друг.

Она што е најфасцинантно во целиот проблем, за кој научниците само се сплеткуваат со години, е дека неговото решавање може да отвори нова врата во компјутерската безбедност и енкрипцијата. Ако ние знаеме на кој начин проблемите усложнуваат, односно алгоритмите за нивно решавање усложнуваат, тогаш многу подобро ќе знаеме како да измислиме сложени шифри, пасворди…Криптографијата веќе се бави со 13-цифрени броеви кои содржат и букви, но да се открие метод кој ја пробива сложеноста наместо да ги проверува комбинациите од 13^n e многу потешоко.

Тогаш експоненцијалноста на проблемите не би била проблем бидејќи би го знаеле начинот на којшто сето тоа се случува и дали и до каде оваа комплексност може да се реши. Сега за сега, нашите можности се ограничени. Ако на најбрзите суперкомпјутери денеска им дадете равенка со 2 на n-та и тој n биде поголем од 300, тогаш тој број веќе го надминува борот на атоми во универзумот за кој знаеме. Тоа значи дека за да го реши проблемот суперкомпјутерот ќе врти и ќе врти…за некои проблеми ќе врти и повеќе од возраста на универзумот, која е 13,7 милијарди години.

Легендарниот математичар Курт Годел забележал и нешто друго. Дека самата математика како наука можеме да ја опишеме како самиот овој проблем П спроти НП. Тој на својот колега Џон Фон Нојман во писмо во 1956 година му напишал дека ако П=НП тоа „ќе има последици од најголемо значење. Имено, тоа очигледно би значело дека … менталната работа на математичарот во врска со прашањата да-или-не може целосно да се замени со машина“.